You're Reading: How Elevation Effects Golf Ball Flight
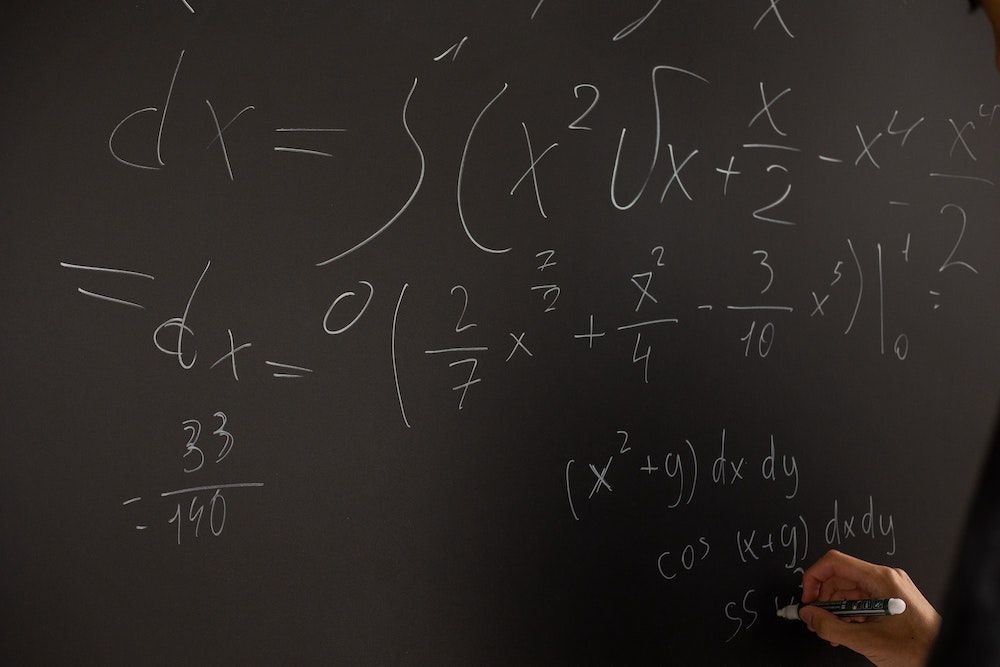
An explanation of the projectile motion of a golf ball under flat conditions was covered previously here. In this article, the goal is to include slope into the equation. In other words, what happens when you are hitting to an elevated green?
A simple heuristic is that a yard in elevation change results in a one yard difference in carry distance. Thus, if the green is situated 5 yards above from where you are hitting your approach and the raw yardage is 155 yards, the adjusted distance is 160 yards. Similarly, if the green is 5 yards downhill, the true carry distance will shorten to 150 yards.
Moving beyond a simple heuristic, it is possible to represent the adjusted distance down to a science — physics. Unfortunately, the straightforward kinematic equations used before are insufficient. The primary reason for this is that those equations do not account for spin. While spin also causes a golf ball to go farther, this effect is more noticeable with longer clubs and not as much for a 7 iron. However, regardless of the club used, the lift attributable to dimples leads to a significant increase in apex. Why is this important for understanding elevation changes? A higher apex means that the overall flight of the golf ball will be steeper. Therefore, the distance traveled horizontally will be less for each yard traveled vertically than it would be for a shallower flight.
An elevation increase of 10 feet essentially means that we can subtract any horizontal distance that would have been achieved if the ball was descending its last 10 feet under flat conditions. With a steep flight, little horizontal distance would have been achieved in the last 10 feet anyway. Ultimately, then, with dimples, the effect of elevation is more subdued than without.
Let’s see what happens when we use the kinematic equations ignoring dimples and spin. In the below box, data on the LPGA Tour average 7-iron ball speed and launch angle from Trackman are used.
Note that the elevation change of 10 feet is represented on the left side of the equation in step 1. Note further that the 10 feet is divided by 5280, performing the conversion to miles which is important to keep consistent units.
As alluded to above, the effect of elevation change is much more significant due to the shallower flight without dimples. Instead of a 1:1 ratio between elevation change and carry distance, the ratio is 1:3, where a foot in elevation change equates to a yard difference in carry distance.
Constructing the equation for golf ball flight that factors dimples and spin is outside the scope of this article. Nevertheless, kinematic equations themselves can provide insight that you can apply out on the course.
The following graph plots the flights of an average pitching wedge, 7 iron, and driver on the LPGA.
Naturally, the pitching wedge has the steepest flight whereas those of the 7 iron and driver are shallower. As can be seen, a 10-foot elevation change has the following effects on each of the clubs: 128.82 yards to 121.47 yards (7.35), 148.40 yards to 137.99 yards (10.41), 194.22 yards to 178.78 yards (15.44). The shallower the flight, the more significant the loss carry distance. Furthermore, percentage-wise, the pitching wedge lost 7.35 / 128.82 = 5.7% in carry distance, the 7 iron lost 10.41 / 148.40 = 7.0% in carry distance, and the driver lost 15.44 / 194.22 = 7.9%.
Despite the fact that we are not considering dimples and that these values are greater than reality, the same concept holds true that elevation changes are more impactful with longer clubs. Another observation is that there is an exponential relationship between elevation change and adjusted carry distance. This is due to parabolic and thus exponential nature of the flights as shown in the graph. After its apex, the golf ball’s flight increasingly grows steeper. For the 7 iron, a 5-foot elevation change decreases carry distance from 148.40 yards to 143.39 yards (5.01). An additional 5 feet drops carry distance from 143.39 yards to 137.99 yards (5.40). Following this progression, there is an additional 9.17-yard loss in carry from 25 feet to 30 feet elevation.
Thus, if you have a shot with a significant elevation change on the course, understand that the amount for which to adjust will not obey a simple multiplication exercise where the assumption is that a 15-foot elevated green will have thrice the loss yards as an elevation of 5 feet. This is not the case. The lost yards in carry will be in fact be greater.
Dimples are critical. Their presence on a golf ball increases flight distance and height. With dimples or without, however, we know that shallower flights (usually linked to longer clubs) will be more affected by elevation changes than will steeper flights. We also know that each additional unit change in elevation will have an increasingly greater effect on carry distance.
Finally, it is important to note that the discussion in this article revolves around carry distance. As golfers know, roll is also important. In brief, hitting to an elevated green will lead to more roll despite less carry. This is because the flight is not as steep as it would be when hitting the ground under flat conditions. Similarly, there will be less roll when hitting downhill as the flight becomes steeper the longer it is in the air.